本文共 2217 字,大约阅读时间需要 7 分钟。
前言
成为优秀的架构师是大部分初中级工程师的阶段性目标。优秀的架构师往往具备七种核心能力:编程能力、调试能力、编译部署能力、性能优化能力、业务架构能力、在线运维能力、项目管理能力和规划能力。
这几种能力之间的关系大概如下图。编程能力、调试能力和编译部署能力属于最基础的能力。不能精通掌握这三种能力,很难在性能优化能力和业务架构能力方面有所成就。具备了一定的性能优化能力和业务架构能力之后,才能在线运维能力和项目管理能力方面表现优越。团队管理能力是最高能力,它对项目管理能力的依赖度更大。

1. 消息的可靠性投递
在使用 RabbitMQ 的时候,作为消息发送方希望杜绝任何消息丢失或者投递失败场景。
RabbitMQ 为我们提供了两种方式用来控制消息的投递可靠性模式。
confirm 确认模式:当消息从 producer 发送到 exchange 则会执行 confirmCallback中的confirm方法。
return 退回模式:当消息发送给Exchange后, Exchange将消息路由到queue失败会执行ReturnCallBack。
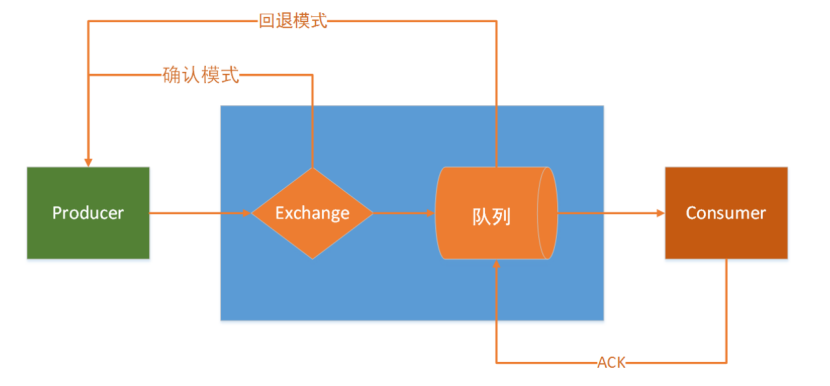
确认模式会返回{1.相关配置信息, 2.交换机是否成功接收到消息 , true 成功 false失败 3.失败原因 }
回退模式会返回{1.消息对象,2.错误码,3.错误信息,4.交换机名称,5.路由键}
2.Consumer ACK(消费者 ACK)
ack指Acknowledge,确认。 表示消费端收到消息后的确认方式。
RabbitMQ提供三种确认方式:
自动确认: acknowledge=“none” 当消息一旦被Consumer接收到,则自动确认收到,并将相应 message 从 RabbitMQ 的消息缓存中移除。
手动确认: acknowledge=“manual” 如果出现异常,则调用channel.basicNack()方法,让其自动重新发送消息。
根据异常情况确认:acknowledge=“auto”。
3. 消息过期(TTL)
TTL 全称 Time To Live(存活时间/过期时间)。当消息到达存活时间后,还没有被消费,会被自动清除。
RabbitMQ可以对消息设置过期时间,也可以对整个队列(Queue)设置过期时间。
消息过期, 可以让队列统一过期, 也可以让它单独的消息过期。
4. 死信队列
死信队列,英文缩写:DLX 。Dead Letter Exchange(死信交换机),当消息成为Dead message (死信)后,可以被重新发送到另一个交换机,这个交换机就是DLX。
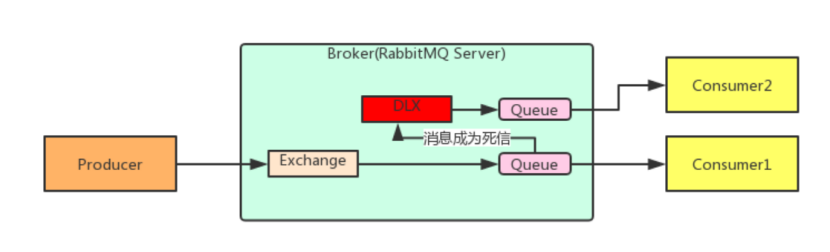
消息成为死信的三种情况:
1.队列消息长度到达限制;
2.消费者拒接消费消息,并且不把消息重新放入原目标队列;
3.原队列存在消息过期设置,消息到达超时时间未被消费;
死信队列和死信交换机:
死信队列和死信交换机与正常的队列和交换机一模一样, 没有任何区别 !!
如何实现队列与死信交换机绑定 , 给队列设置如下参数:
-
x-dead-letter-exchange : 设置死信交换机
-
x-dead-letter-routing-key : 设置死信路由key
5. 延迟队列
消息进入队列后不会立即被消费,只有到达指定时间后,才会被消费。 例如:

延迟队列是一个很强大的功能 , 但是在RabbitMQ中并没有提供延迟队列功能。
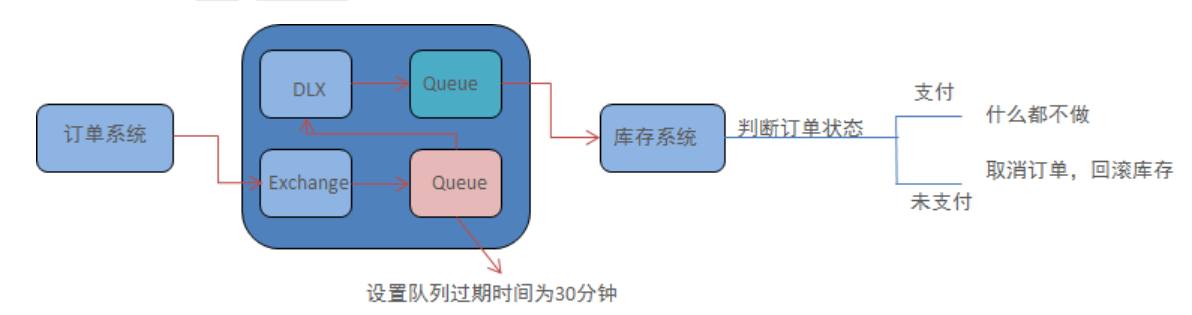
可以使用:TTL(消息过期)+死信队列组合实现延迟队列的效果。
实现流程图如下 :
6. 消费端限流
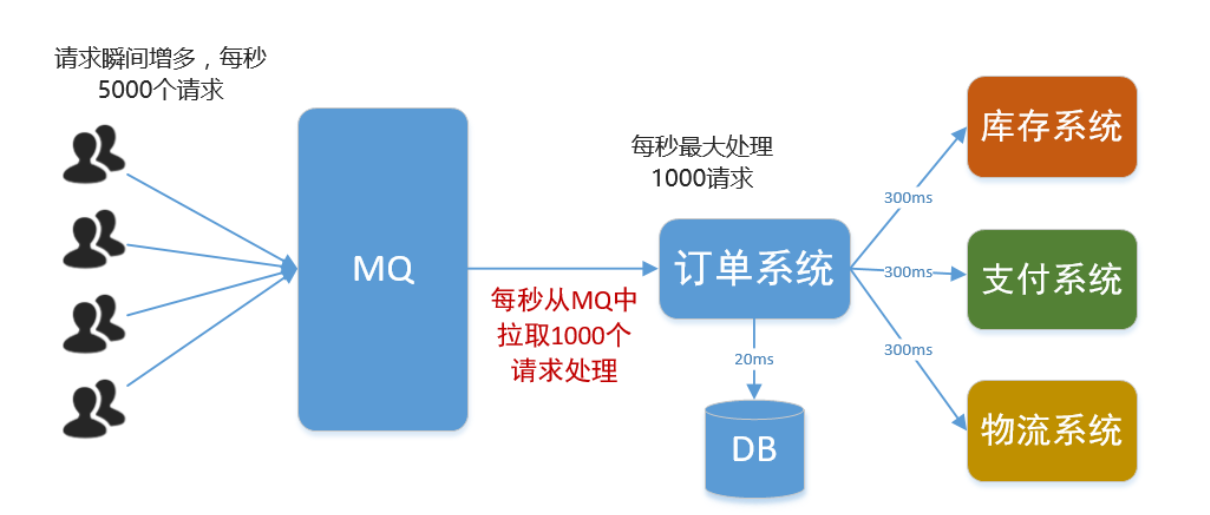
当系统峰值比较高的时候 , 我们我们可以使用RabbitMQ实现削峰填谷, 让我们系统处理的请求更加平稳
实现步骤
-
设置akc机制为手动确认
-
配置监听容器
7.RabbitMQ应用问题 (消息补偿机制)
我们通过之前的消息可靠性投递 , ACK 确认机制 , 以及死信队列 , 基本上已经能够保证消息投递成功了 !
为什么还要消息补偿机制呢? 难道消息还会丢失,没错,系统是在一个复杂的环境,不要想的太简单了,虽然以上的三种方案,基本可以保证消息的高可用不丢失的问题,但是作为有追求的程序员来讲,要绝对保证我的系统的稳定性,有一种危机意识。
比如:持久化的消息,保存到硬盘过程中,当前队列节点挂了,存储节点硬盘又坏了,消息丢了,怎么办?
产线网络环境太复杂,所以不知数太多,所以要做消息补偿机制 !
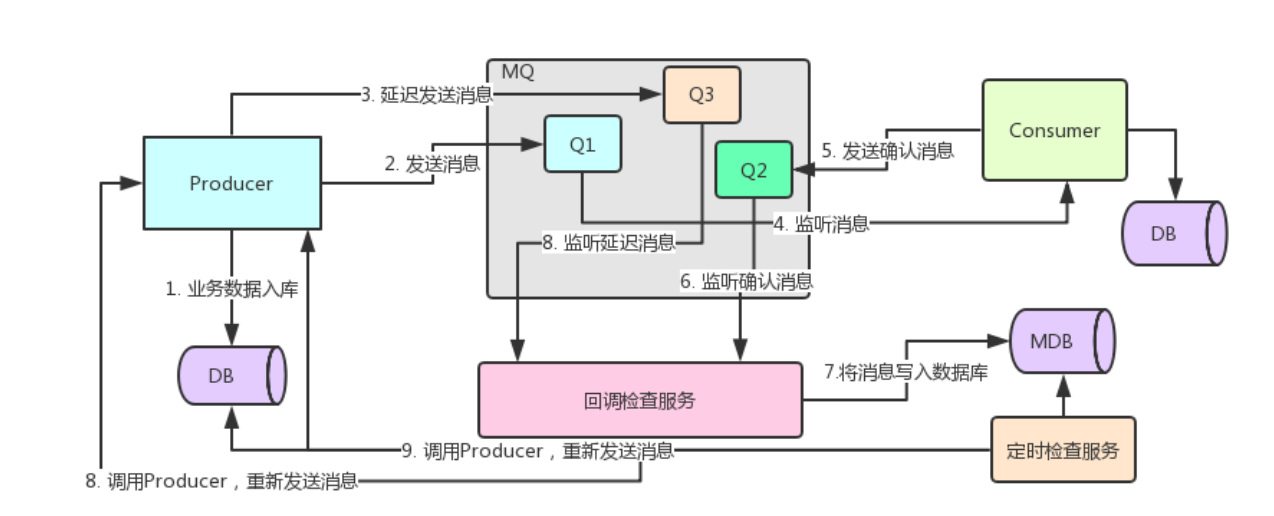
消息补偿机制需要建立在业务数据库和MQ数据库的基础之上 , 当我们发送消息时 , 需要同时将消息数据保存在数据库中, 两者的状态必须记录。 然后通过业务数据库和MQ数据库的对比检查消费是否成功,不成功,进行消息补偿措施,重新发送消息处理
一线互联网大厂Java核心面试题库
息处理
[外链图片转存中…(img-ZB9siwA2-1620366210434)]
一线互联网大厂Java核心面试题库
[外链图片转存中…(img-dKflDiHj-1620366210435)]
正逢面试跳槽季,给大家整理了大厂问到的一些面试真题,由于文章长度限制,只给大家展示了部分题目,更多Java基础、异常、集合、并发编程、JVM、Spring全家桶、MyBatis、Redis、数据库、中间件MQ、Dubbo、Linux、Tomcat、ZooKeeper、Netty等等…已整理上传在我的,并会持续更新…感兴趣的朋友可以看看支持一波!
转载地址:http://toxwz.baihongyu.com/